计算机组成:无符号数和有符号数

[TOC]
1.无符号数
直接用二进制表示。
寄存器的位数反映了无符号数的表示范围。
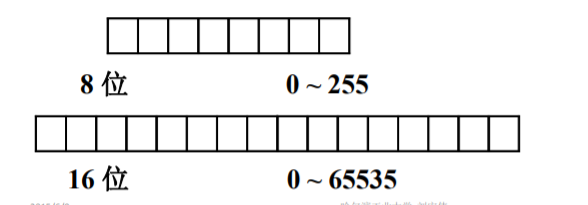
2.有符号数
1.机器数与真值
保存在计算机中的数字我们称为机器数 ,我们平时用的带有符号的真实的值称为真值 。在计算机中用0或1 表示数字的符号 。
大家注意,在计算机中没有专门的硬件用于表示小数点,计算机中的小数点都是以约定的方式给出的。
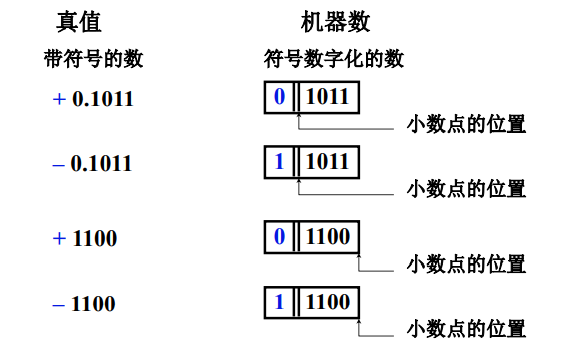
2.原码表示法
整数
我们这里以数学的方式给出原码表示法的定义
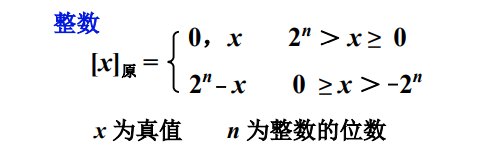
注意到对于一个位数为 n 的正整数,即使所有数位上的值都是 1 ,这是值达到最大值 $$2^n-1$$ ,所以上面第一个范围是$$ 2^n>x>=0$$
根据上面公式可以看出,如果 $$x$$ 的值为 0 ,则有两种表示方式 。
下面是一个具体的实例:
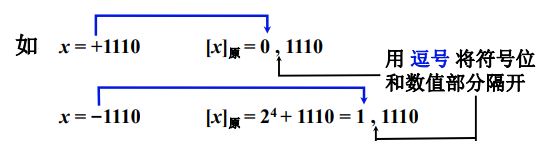
我们不难发现,
- 对于正整数而言,取符号位为 0 ,后面直接加上真值的二进制表示即可
- 对于负整数而言,取符号位为 1,后面直接加上真值的绝对值的二进制表示即可
由此,我们得出结论:原码是带符号的绝对值表示!
小数
接下来我们来看一下小数的原码表示,同样不难发现,小数 0 同样有两种表示方法。
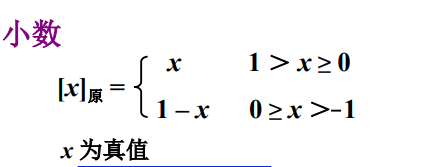
我们再来看四个例子

我们不难发现,对于小数,正小数的真值和原码表示的格式 是一致的,但是这里大家要注意,二者小数点前面的 0 的含义确完全不同!
另外,由于原码表示是要存储在计算机中的,所以想要求得某个真值的原码表示,必须已知机器数的数值部分的长度才行。
我们再来一起做几组练习



通过最后一个例子,我们不难验证,$$x=0$$ 的原码有两个不同的值!
最后,我们对原码做一个总结。
不难发现,原码表示法的特点是:简单 、直观 !但是,使用原码做加法运算的时候,会出现一些问题:


这样不仅需要加法器,还需要减法器,同时结果的处理情况也比较复杂 ,我们不禁要想,能不能只做加法 ?
具体做法是找到一个与负数等价的正数来代替这个负数 ,从而将减法运算变为加法运算 !这就产生了补码 的概念。
3.补码表示法
1.补的概念
我们都有过给时钟调整时间的经验,比如现在时钟表针指向 6 时,我想把它调整至 3 时,很容易想到有两种不同的做法 能够达到目标!
- 逆时针拨动 3 小时,记为 -3
- 顺时针拨动 9 小时,记为 +9
上面两种操作虽然不同,但是最终达到的结果是一致的。我们可以说**$$-3$$ 与$$+9$$ 在模 12 的条件下是相等的** (模12的意思就是只看余数)!仔细看一下这两个数字,我们是不是已经成功地把负数$$-3$$ 用正数$$+9$$ 代替了?
具体可以看一下这张图片,其实这就是补码 的来历~
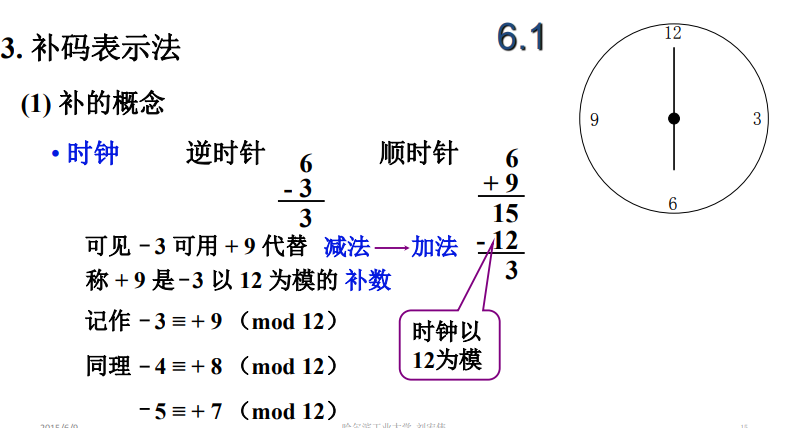
不难发现,当一个正数和一个负数互补的时候,它们两个之和正好等于模数 。
在下图的例子中,我们考虑怎么样从$$1011$$ 运算得到 $$0000$$ ?
- 第一种方法,减去 1011
- 第二种方法,加上 0101,进位自然舍去
在上面的例子中,**-0100 的补数其实就是 +0101**

2.一个小例子
首先,来看两个互为补数的整数$$-1011$$ 与$$+0101$$ ,换成二进制是 -11 和 +5,不难发现,这两个数是关于 16 互补的,也就是在 模16取余数的情况下是相等的。
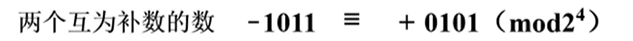
我们接下来的任务是把这两个真值变为补数表示,从而可以在计算机中存储。
对这两个数字分别加上模(16),得到下面的情况:
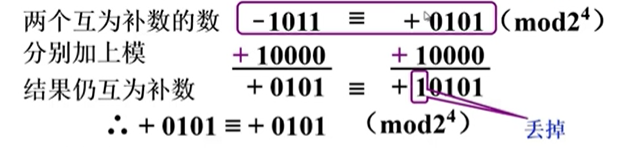
注意,在第二个数字加上16后会溢出,我们直接把超过四位的数字扔掉,于是得到了 +0101的补数是 0101 ,同时,细心的你一定也会发现,**-1011的补数也是0101!,这就出现了问题!0101到底是表示哪个真值?**
于是我们在得到的补数的最前面再加上一位符号位用来确认!而增加的这一位符号位的权值是$$2^n$$ ,也就相当于我们**又加了一个$$2^n$$ ** ,这下总算可以区分上面的两个真值了。
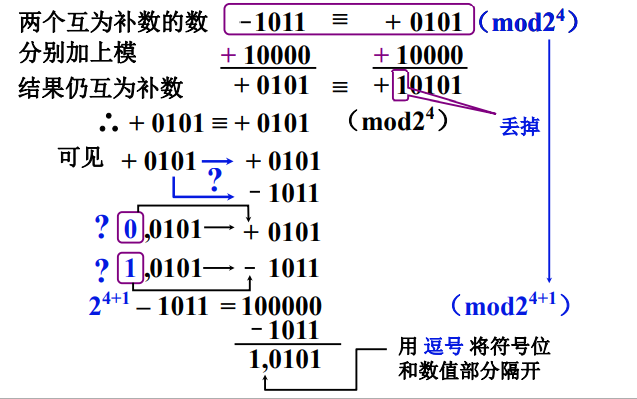
注意在上面的过程中,我们一共加了两次$$2^n$$ ** ,所以最后的结果就是直接模$$2^{n+1}$$ ** !
3.补码的定义
1.整数
通过前面的小例子,我们已经初步接触到了补码,现在给出具体的定义

举个例子:

2.小数
小数补码的定义:
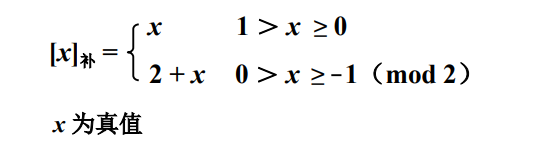
举例:

这里要注意机器数规定长度的限制!
另外,这里的补码处理是以模2进行的。如果模2,小数点前面1位;如果模4,小数点前面2位,都是可以的。
4.求补码的快捷方式
我们考虑对$$x=-1010$$ 求补码表示,根据上面的定义公式,真值是4位,所以$$2^{4+1}$$ , 也就是如下图所示:

所以补码表示就是$$1,0110$$ ,这一点是很清晰的!
从另一个角度来看:
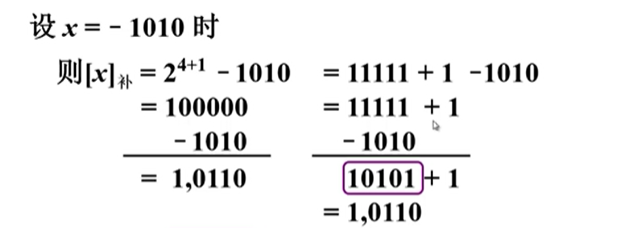
用$$11111$$ 减去真值的绝对值,其实就是对每一位取反 ,然后再加上 1 就得到了补码表示。
所以,负数求补码的方法总结一下就是:
- 符号位不变
- 数值位取反加一

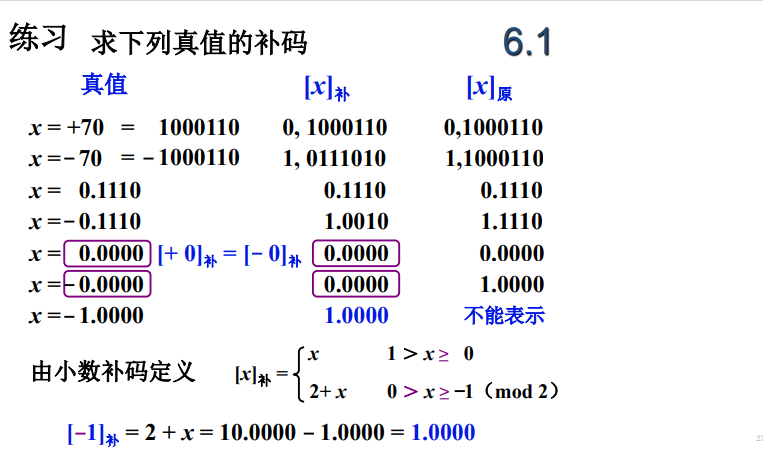
4.举例



注意一个小规律:从补码转换为原码的操作同样是:
- 符号位不变
- 数值位取反加一

最后,补码最重要的是能够把减法变成加法 ,这才是最重要的!
4.反码表示法
1.整数定义
反码的定义相比补码要简单一点,对于正数,两者是一样的,对于负数,仅仅是把补码要加的那个$$1$$ 不加了,单纯对数值位取反! ,这样的话,用严格的数学定义,就是$$模2^{n+1}-1$$ 了。

来看两个例子:
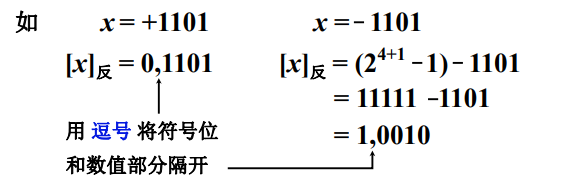
2.小数定义
对于小数的反码定义,其实和整数一致,但是要注意数值位最后面的那个 $$“1”$$ 其实是$$2-2^{-n}$$ 。
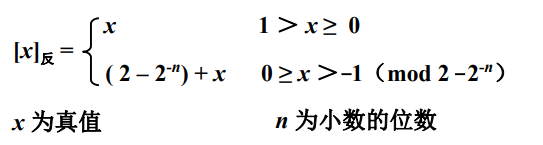
举例如下:

再看几个小例子:
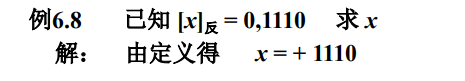
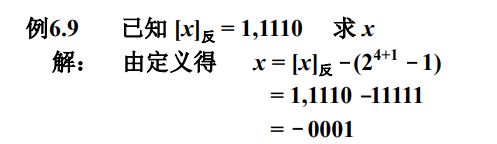

注意$$+0$$ 与$$-0$$ 的反码机器数表示是不同的
5.三种机器数的小结


三种机器数表示的范围如下(以8位机器数字长为例):
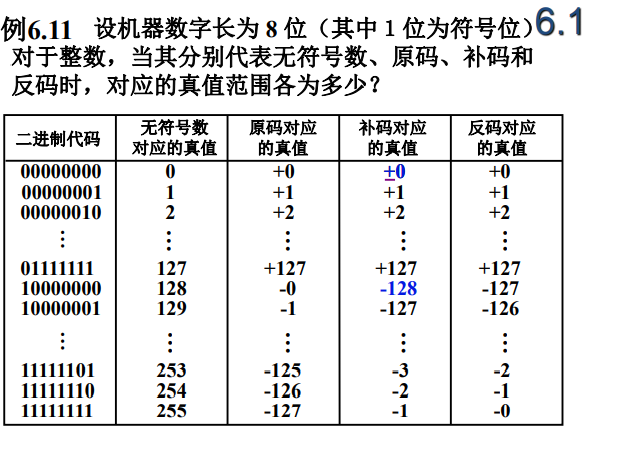
接下来我们再来看一个比较重要的结论:
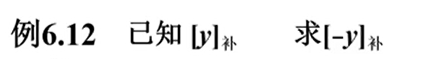
分两种情况讨论:y 为正数和 y 为 负数
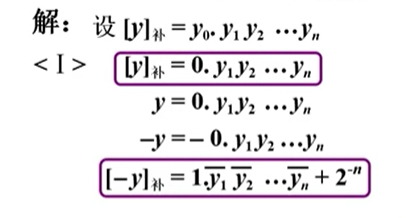
得到下面这个结论:

对于第二种情况:
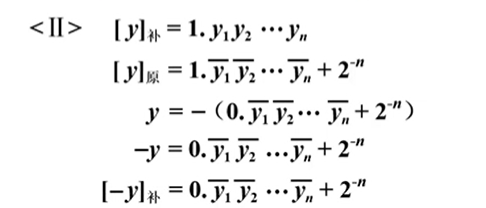
得到下面结论:

综上所述:**$$[y]{补}$$ 连同符号位在内,每位取反,末位加$$1$$ ,即得到$$[-y]{补}$$ !** ,这是个十分重要的结论!
6.移码表示法
1.移码定义
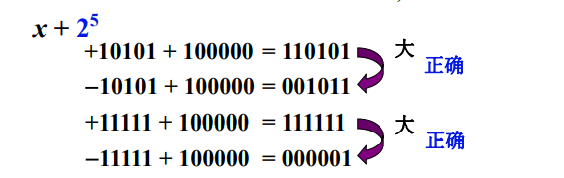
移码的提出是为了解决补码表示很难直接判断真值大小这样一个问题。举例如下:

因为在补码表示中,负数第一个符号位是 1,正数第一个符号位是 0 ,而$$1>0$$ ,这样直接使用补码进行大小判断得到的结果是不可靠的,所以我们引进了移码的表示方法。通过对真值加上特定的数字进行“平移”,从而解决这一问题
接来我们给出移码的定义:
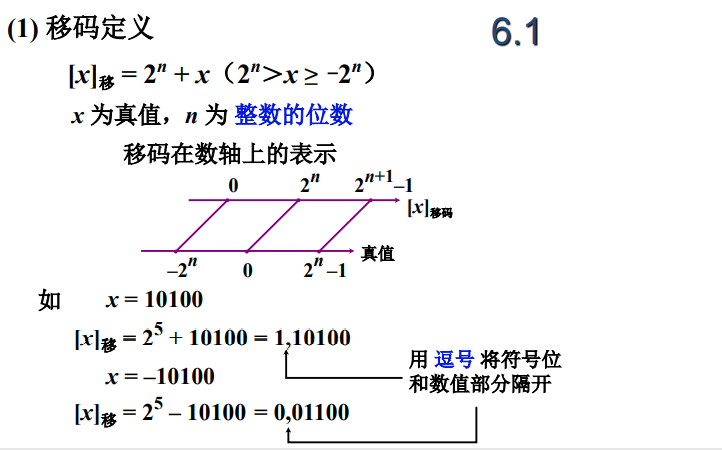
简单来说,移码中的“移”就是在数轴上进行平移
2.移码和补码的比较

结合示例很容易发现补码和移码只差一个符号位 ,从而完美的解决了比较大小的问题。
3.真值、补码和移码的对照表
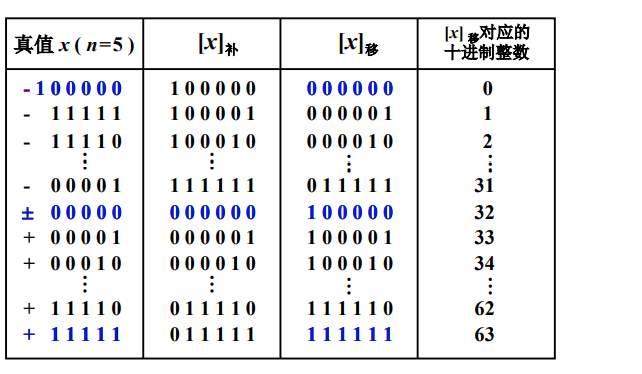
4.移码的特点

另外两点值得注意的是:
- 在移码的平移过程中,最小的真值被移动到了位置 0
- 移码主要用在表示浮点数的阶码




