有向环、拓扑排序与Kosaraju算法

25张图详解有向环、拓扑排序与Kosaraju算法。有向环如何检测？拓扑排序的原理？Kosaraju算法又是如何得到的？本文告诉你答案

首先来看一下今天的内容大纲，内容非常多，主要是对算法思路与来源的讲解，图文并茂，希望对你有帮助~

1.有向图的概念和表示

概念

有向图与上一篇文章中的无向图相对，边是有方向的，每条边所连接的两个顶点都是一个有序对，它们的邻接性都是单向的。

一幅有方向的图（或有向图）是由一组顶点和一组有方向的边组成的，每条有方向的边都连接着一对有序的顶点。

其实在有向图的定义这里，我们没有很多要说明的，因为大家会觉得这种定义都是很自然的，但是我们要始终记得有方向这件事！

数据表示

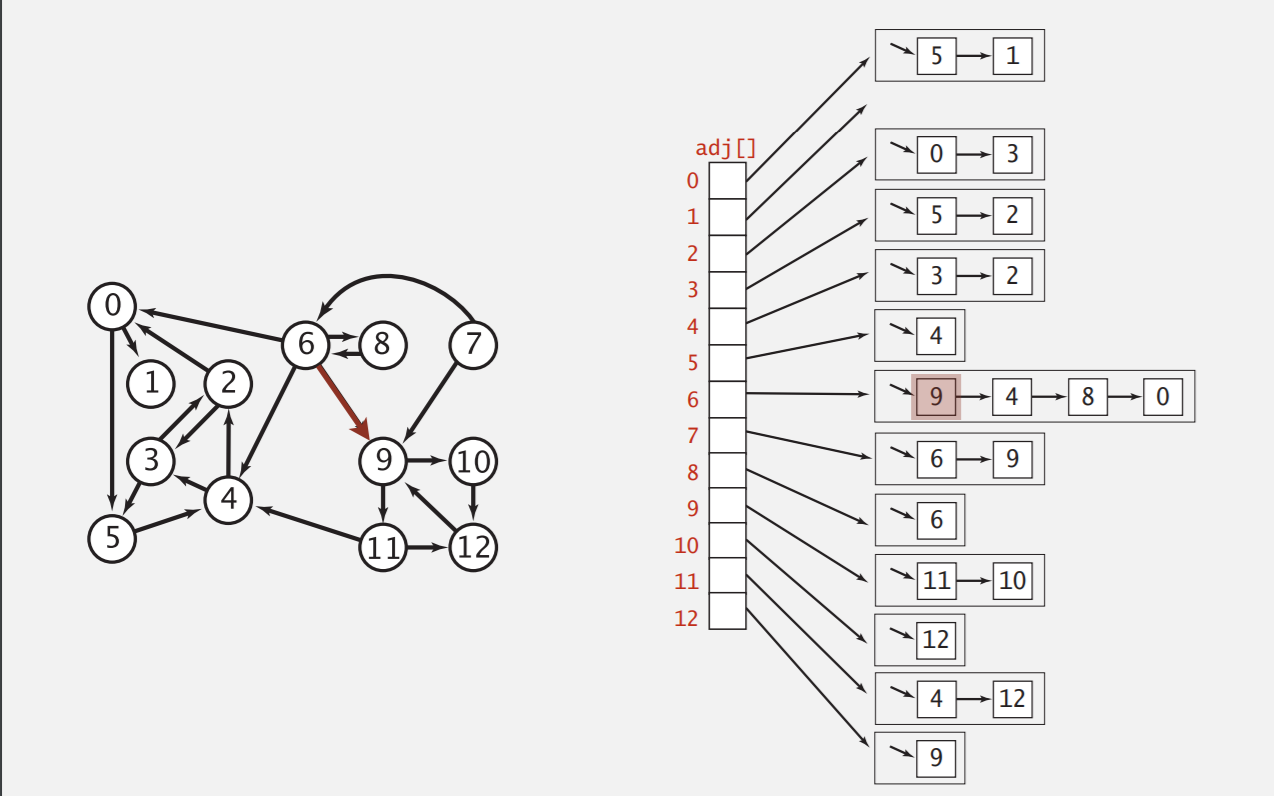
我们依然使用邻接表存储有向图，其中v-->w表示为顶点v的邻接链表中包含一个顶点w。注意因为方向性，这里每条边只出现一次！

我们来看一下有向图的数据结构如何实现，下面给出了一份Digraph类(Directed Graph)

package Graph.Digraph;
import java.util.LinkedList;

public class Digraph{
    private final int V;//顶点数目
    private int E;//边的数目
    private LinkedList<Integer> adj[];//邻接表

    public Digraph(int V){
        //创建邻接表
        //将所有链表初始化为空
        this.V=V;this.E=0;
        adj=new LinkedList[V];
        for(int v=0;v<V;++v){
            adj[v]=new LinkedList<>();
        }
    }

    public int V(){ return V;}//获取顶点数目
    public int E(){ return E;}//获取边的数目

    //注意，只有这里与无向图不同
    public void addEdge(int v,int w){
        adj[v].add(w);//将w添加到v的链表中
        E++;
    }

    public Iterable<Integer> adj(int v){
        return adj[v];
    }

    //获取有向图的取反
    public Digraph reverse(){
        Digraph R=new Digraph(V);
        for(int v=0;v<V;v++){
            for(int w:adj(V))
                R.addEdge(w, v);//改变加入的顺序
        }
        return R;
    }
}

如果你已经掌握了无向图的数据表示，你会发现有向图只是改了个名字而已，只有两处需要注意的地方：addEdge(v,w)方法与reverse()方法。在添加一条边时因为有了方向，我们只需要在邻接表中增加一次；reverse()方法能够返回一幅图的取反（即每个方向都颠倒过来），它会在以后的应用中发挥作用，现在我们只要有个印象就行。

2.有向图的可达性

在无向图（上一篇文章）中，我们使用深度优先搜索可以找到一条路径，使用广度优先搜索可以找到两点间的最短路径。仔细想一下，它们是否对有向图适用呢？是的，同样的代码就可以完成这个任务，我们不需要做任何的改动（除了Graph换成Digraph）。

因为这些内容在上篇文章中都已经详细介绍过，所以就不展开了，有兴趣的话可以翻一下上篇文章，有详细的图示讲解。

3.环和有向无环图

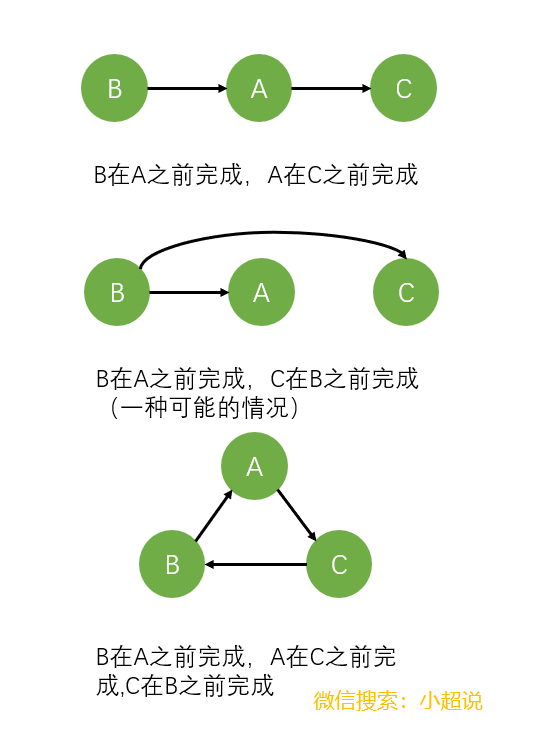
我们在实际生活中可能会面临这样一个问题：优先级限制下的调度问题。说人话就是你需要做一些事情，比如A,B,C，但是做这三件事情有一定的顺序限制，做B之前必须完成A,做C之前必须完成B…………你的任务就是给出一个解决方案（如何安排各种事情的顺序），使得限制都不冲突。

如上图，第一种和第二种情况都比较好办，但是第三种？是不是哪里出了问题！！！

对于上面的调度问题，我们可以通过有向图来抽象，顶点表示任务，箭头的方向表示优先级。不难发现，只要有向图中存在有向环，任务调度问题就不可能实现！所以，我们下面要解决两个问题：

• 如何检测有向环（只检查存在性，不考虑有多少个）
• 对于一个不存在有向环的有向图，如何排序找到解决方案（任务调度问题）

1.寻找有向环

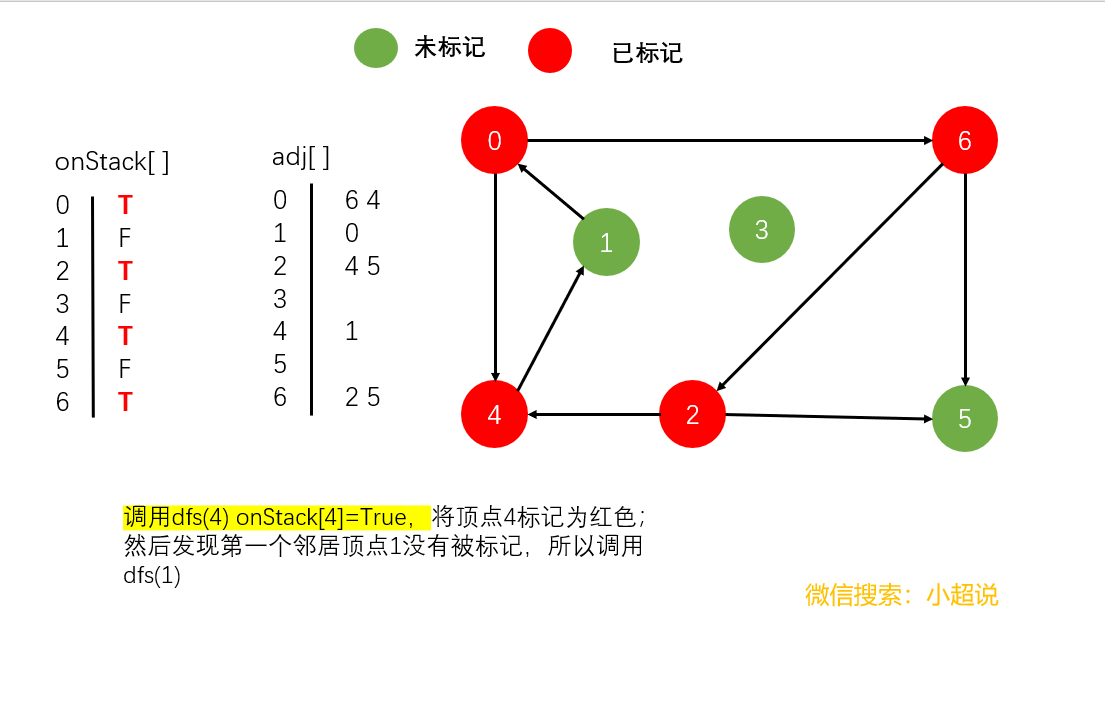
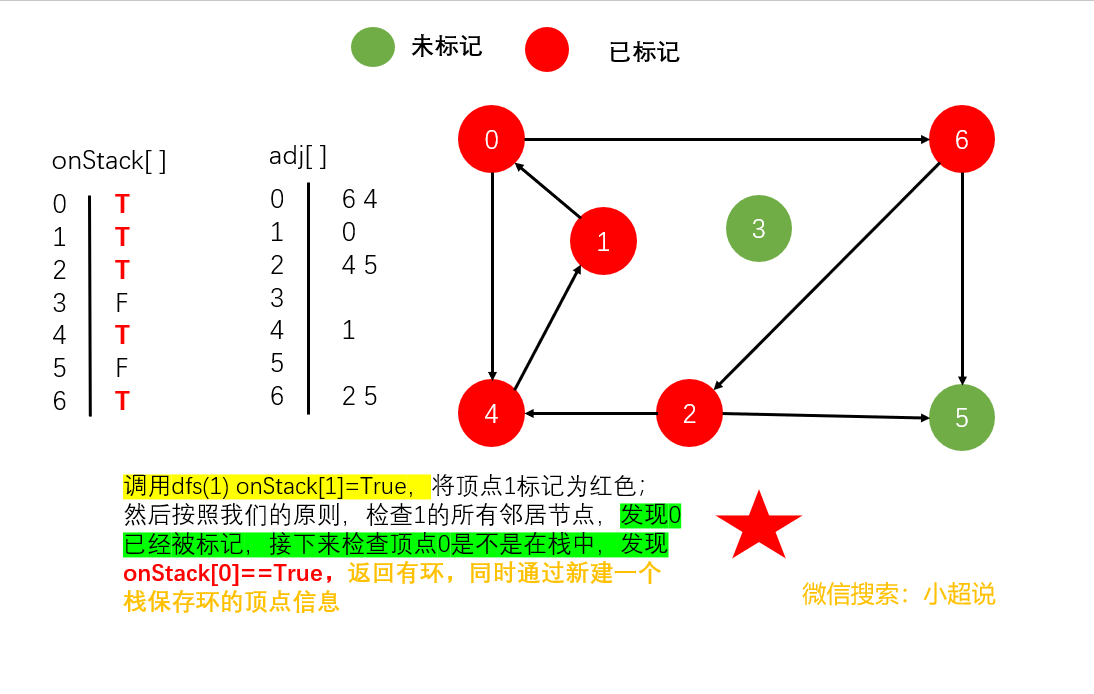
我们的解决方案是采用深度优先搜索。因为由系统维护的递归调用栈表示的正是“当前”正在遍历的有向路径。一旦我们找到了一条有向边v-->w,并且w已经存在于栈中，就找到了一个环。因为栈表示的是一条由w指向v的有向路径，而v-->w正好补全了这个环。同时，如果没有找到这样的边，则意味着这幅有向边是无环的。

我们所使用的数据结构：

• 基本的dfs算法
• 新增一个onStack[]数组用来显式地记录栈上的顶点（即一个顶点是否在栈上）

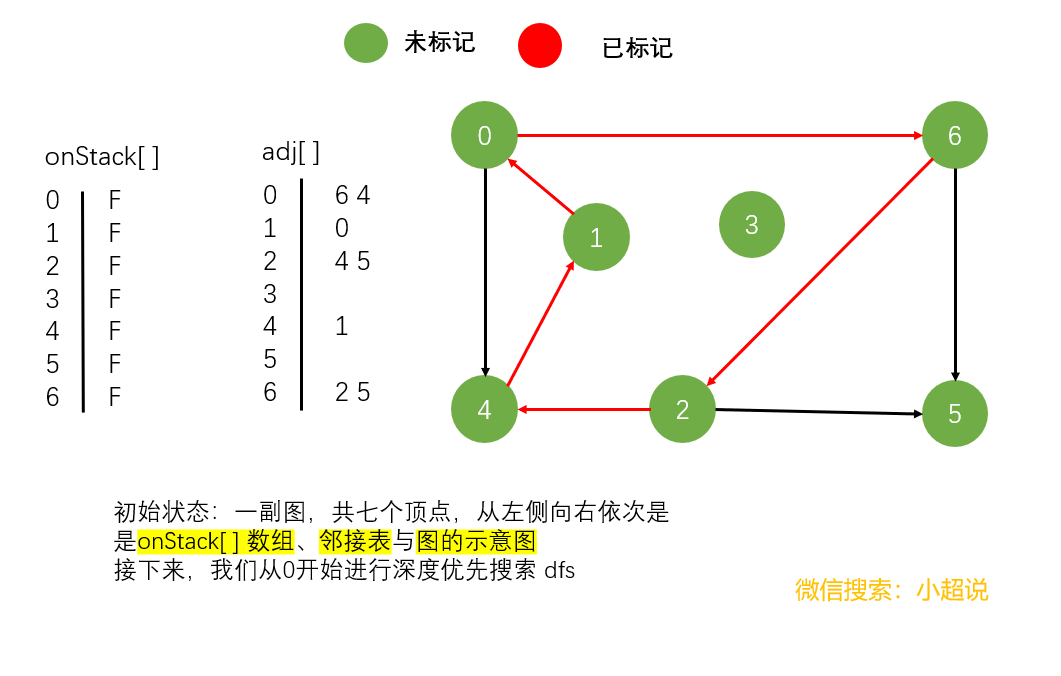
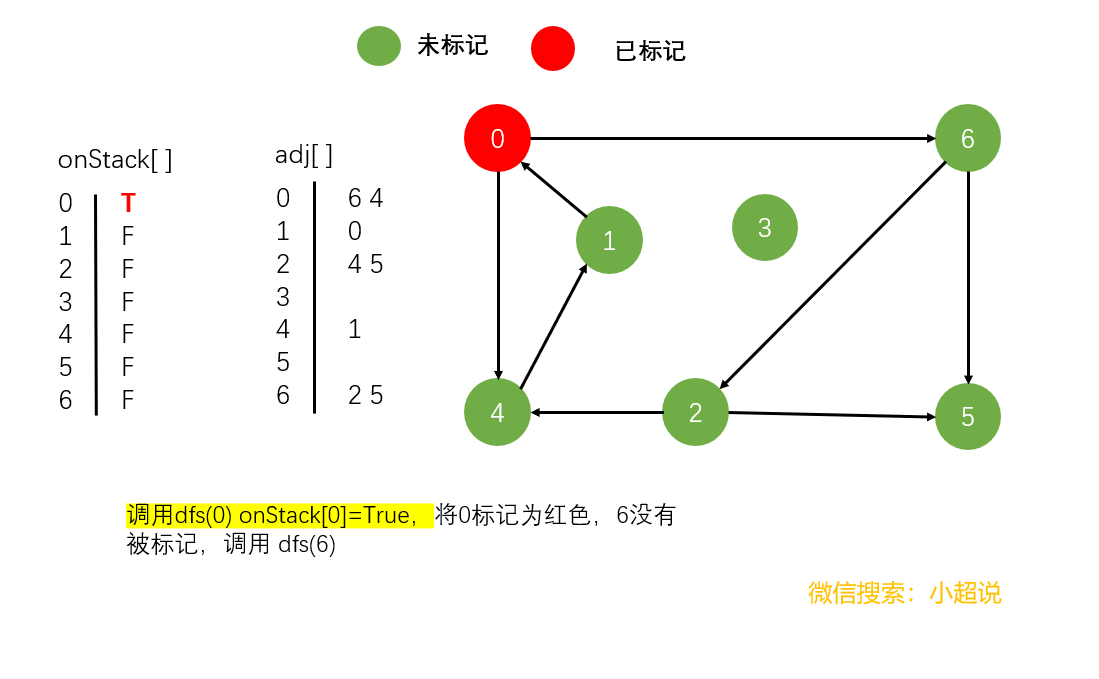
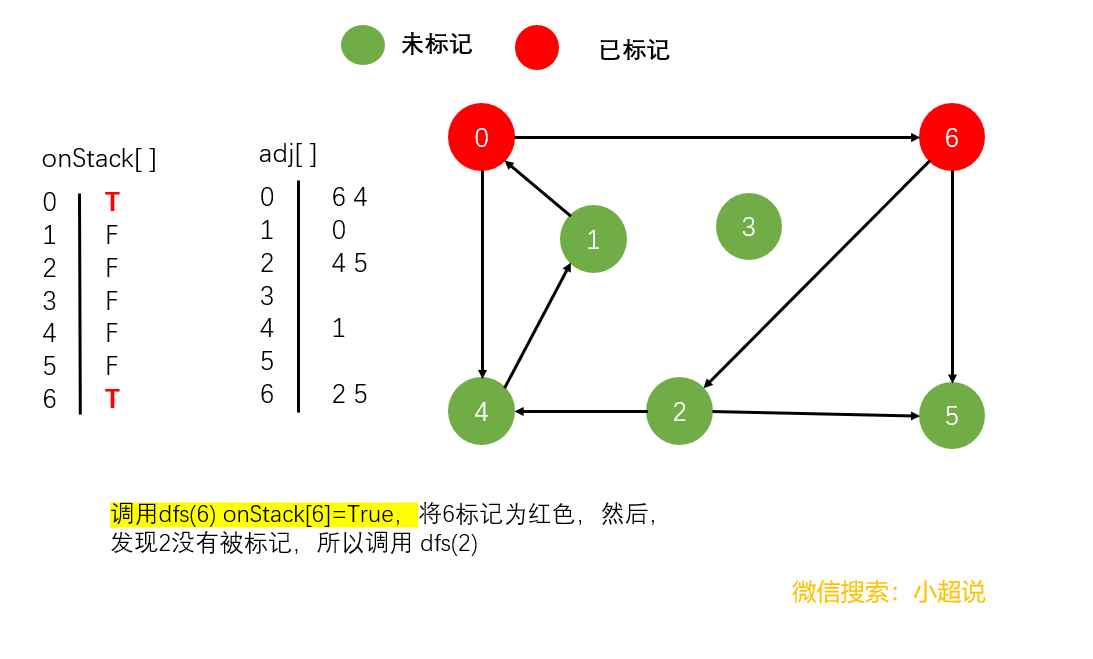
我们还是以一个具体的过程为例讲解

具体的代码我想已经难不倒你了，我们一起来看看吧

package Graph.Digraph;

import java.util.Stack;

public class DirectedCycle {
    private boolean [] marked;
    private int [] edgeTo;
    private Stack<Integer> cycle;//有向环中的所有顶点（如果存在）
    private boolean[] onStack; //递归调用的栈上的所有顶点

    public DirectedCycle(Digraph G){
        onStack=new boolean[G.V()];
        edgeTo=new int[G.V()];
        marked=new boolean[G.V()];
        
        for(int v=0;v<G.V();v++){
            if(!marked[v]) dfs(G,v);
        }
    }

    private void dfs(Digraph G,int v){
        onStack[v]=true;//进入dfs时，顶点v入栈
        marked[v]=true;
        for(int w:G.adj(v)){
            if(this.hasCycle()) return;
            else if(!marked[w]){
                edgeTo[w]=v;dfs(G,w);
            }
            else if(onStack[w]){
                //重点
                cycle=new Stack<Integer>();
                for(int x=v;x!=w;x=edgeTo[x])
                    cycle.push(x);

                cycle.push(w);
                cycle.push(v);
            }
        }
        //退出dfs时，将顶点v出栈
        onStack[v]=false;
    }

    public boolean hasCycle(){
        return cycle!=null;
    }

    public Iterable<Integer> cycle(){
        return cycle;
    }
}

该类为标准的递归 dfs() 方法添加了一个布尔类型的数组 onStack[] 来保存递归调用期间栈上的
所有顶点。当它找到一条边 v → w 且 w 在栈中时，它就找到了一个有向环。环上的所有顶点可以通过
edgeTo[] 中的链接得到。

在执行 dfs(G,v) 时，查找的是一条由起点到 v 的有向路径。要保存这条路径, DirectedCycle维护了一个由顶点索引的数组 onStack[]，以标记递归调用的栈上的所有顶点（在调用
dfs(G,v) 时将 onStack[v] 设为 True，在调用结束时将其设为 false）。DirectedCycle 同时也
使用了一个 edgeTo[] 数组，在找到有向环时返回环中的所有顶点，

2.拓扑排序

如何解决优先级限制下的调度问题？其实这就是拓扑排序

拓扑排序的定义：给定一幅有向图，将所有的顶点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素（或者说明无法做到这一点）

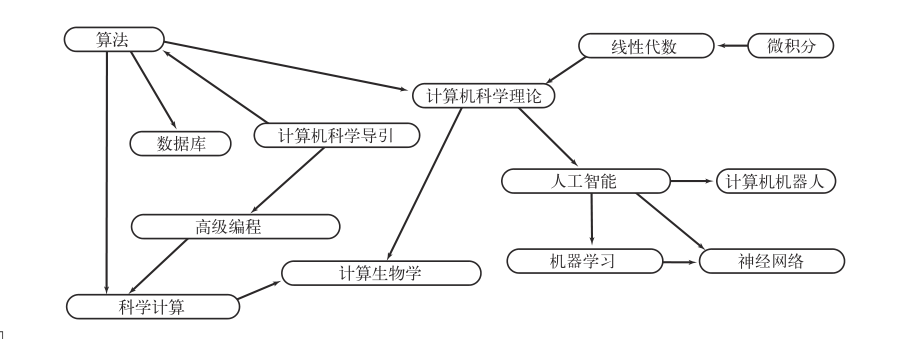
下面是一个典型的例子（排课问题）

它还有一些其他的典型应用，比如：

现在，准备工作已经差不多了，请集中注意力，这里的思想可能不是很好理解。紧跟我的思路。

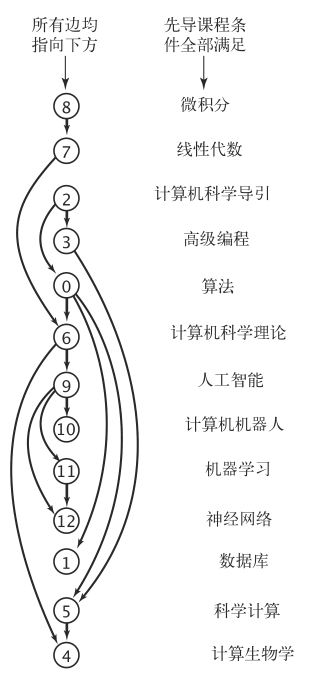
现在首先假设我们有一副有向无环图，确保我们可以进行拓扑排序；通过拓扑排序，我们最终希望得到一组顶点的先后关系，排在前面的元素指向排在后面的元素，也就是对于任意的一条边v——>w，我们得到的结果应该保证顶点v在顶点w前面；

我们使用dfs解决这个问题，在调用dfs(v)时，以下三种情况必有其一：

• dfs(w)已经被调用过且已经返回了（此时w已经被标记）
• dfs(w)已经被调用过且还没有返回（仔细想想这种情况，这是不可能存在的）
• dfs(w)还没有被调用（w还没有被标记），此时情况并不复杂，接下来会调用dfs(w)，然后返回dfs(w)，然后调用dfs(v)

简而言之，我们可以得到一个很重要的结论：**dfs(w)始终会在dfs(v)之前完成。** 换句话说，先完成dfs的顶点排在后面

请确保你完全理解了上面的思想，接下来其实就相对容易了。我们创建一个栈，每当一个顶点dfs完成时，就将这个顶点压入栈。 最后，出栈就是我们需要的顺序

---

其实到这里拓扑排序基本上就已经被我们解决了，不过这里我们拓展一下，给出一些常见的排序方式，其中我们刚才说到的其实叫做逆后序排序。它们都是基于dfs。

• 前序：在递归调用之前将顶点加入队列
• 后序：在递归调用之后将顶点加入队列
• 逆后序：在递归调用之后将顶点压入栈

我们在这里一并实现这三个排序方法，在递归中它们表现得十分简单

package Graph.Digraph;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class DepthFirstOrder {

    private boolean [] marked;
    private Queue<Integer> pre;//所有顶点的前序排列
    private Queue<Integer> post;//所有顶点的后序排列
    private Stack<Integer> reversePost;//所有顶点的逆后序排列

    public DepthFirstOrder(Digraph G){
        pre=new LinkedList<>();
        post=new LinkedList<>();
        reversePost = new Stack<>();

        marked=new boolean[G.V()];

        for(int v=0;v<G.V();v++){
            if(!marked[v]) dfs(G,v);
        }
    }

    private void dfs(Digraph G,int v){
        pre.offer(v);

        marked[v]=true;
        for(int w:G.adj(v))
            if(!marked[w])
                dfs(G, w);
        post.offer(v);
        reversePost.push(v);
    }

    //这里可以不用管
    public Iterable<Integer> pre()  
    {  return pre;  } 
   public Iterable<Integer> post() 
   {  return post;  } 
   public Iterable<Integer> reversePost() 
   {  return reversePost;  }
}

---

恭喜你，到这儿我们已经完全可以实现拓扑排序，下面的Topological类实现了这个功能。在给定的有向图包含环的时候，order()方法返回null,否则会返回一个能够给出拓扑有序的所有顶点的迭代器（当然，你也可以很简单的将排序顶点打印出来）。具体的代码如下：

package Graph.Digraph;

public class Topological {

    private Iterable<Integer> order;//顶点的拓扑顺序

    public Topological(Digraph G){
        //判断给定的图G是否有环
        DirectedCycle cyclefinder=new DirectedCycle(G);
        if(!cyclefinder.hasCycle()){
            DepthFirstOrder dfs=new DepthFirstOrder(G);
            order = dfs.reversePost();
        }
    }

    public Iterable<Integer> order(){
        return order;
    }

    //判断图G是不是有向无环图
    public boolean isDAG(){
        return order!=null;
    }
    
}

到这儿，有向环的检测与拓扑排序的内容就结束了，接下来我们要考虑有向图的强连通性问题

4.强连通分量

1.强连通的定义

回想一下我们在无向图的时候，当时我们就利用深度优先搜索解决了一幅无向图的连通问题。根据深搜能够到达所有连通的顶点，我们很容易解决这个问题。但是，问题变成有向图，就没有那么简单了！下面分别是无向图和有向图的两个例子：

定义。如果两个顶点v和w是互相可达的，则称它们为强连通的。也就是说，既存在一条从 v到w的有向路径，也存在一条从w到v的有向路径。如果一幅有向图中的任意两个顶点都是强
连通的，则称这幅有向图也是强连通的。

以下是另一些强连通的例子：

2.强连通分量

在有向图中，强连通性其实是顶点之间的一种等价关系，因为它有以下性质

• 自反性：任意顶点 v 和自己都是强连通的
• 对称性：如果 v 和 w 是强连通的，那么 w 和 v 也是强连通的
• 传递性：如果 v 和 w 是强连通的且 w 和 x 也是强连通的，那
  么 v 和 x 也是强连通的

因为等价，所以和无向图一样，我们可以将一幅图分为若干个强连通分量，每一个强连通分量中的所有顶点都是强连通的。这样的话，任意给定两个顶点判断它们之间的强连通关系，我们就直接判断它们是否在同一个强连通分量中就可以了！

接下来，我们需要设计一种算法来实现我们的目标————将一幅图分为若干个强连通分量。我们先来总结一下我们的目标：

---

3.Kosaraju算法

Kosaraju算法就是一种经典的解决强连通性问题的算法，它实现很简单，但是不好理解why，希望你打起精神，我希望我能够把它讲明白（也只是希望，我会尽量，如果不清楚的话，强烈建议结合算法4一起食用）

---

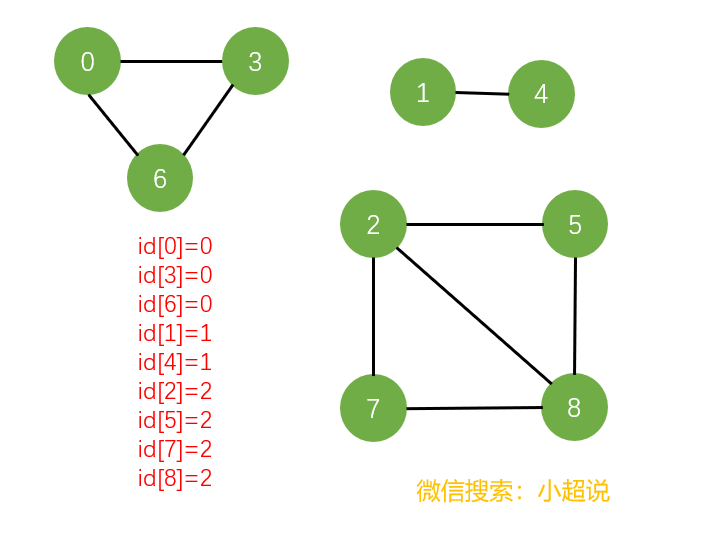
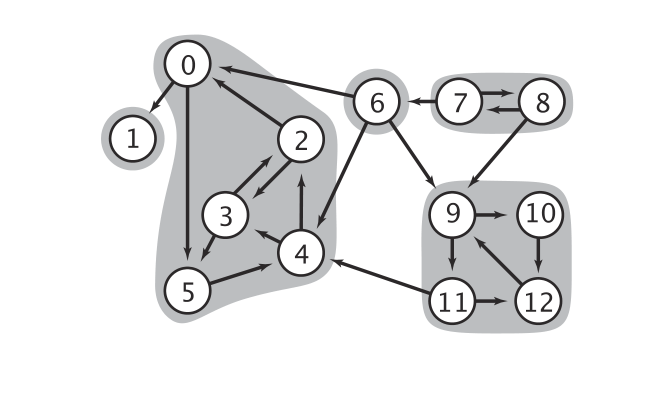
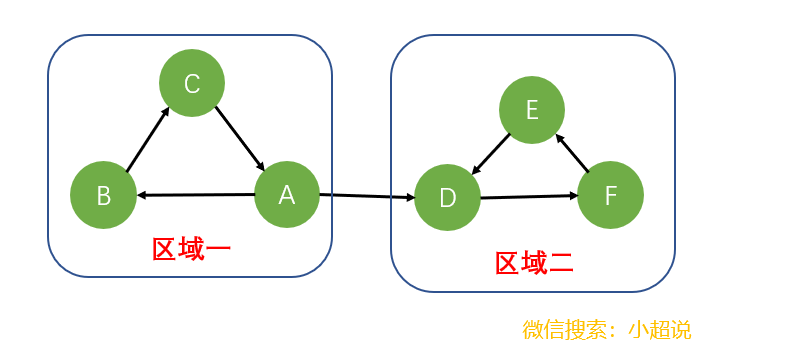
回忆一下我们之前在无向图的部分如何解决连通性问题的，一次dfs能够恰好遍历一个连通分量，所以我们可以通过dfs来计数，获取每个顶点的id[];所以，我们在解决有向图的强连通性问题时，也希望能够利用一次dfs能够恰好遍历一个连通分量的性质；不过，在有向图中，它失效了，来看一下图一：

在图一中，dfs遍历会存在两种情况：

第一种情况：如果dfs的起点时顶点A，那么一次dfs遍历会遍历整个区域一和区域二，但是区域一与区域二并不是强连通的，这就是有向图给我们带来的困难！

第二种情况：如果dfs的起点是顶点D，则第一次dfs会遍历区域二，第二次dfs会遍历区域一，这不就是我们想要的吗？

所以，第二个情况给了我们一个努力的方向！也就是如果我们人为地，将所有的可能的情况都变成第二种情况，事情不就解决了！

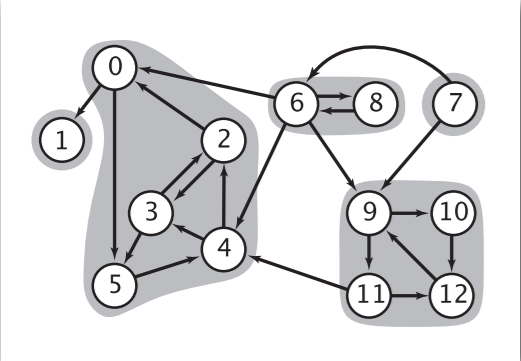
有了方向，那么接下来，我们来看一幅真实的有向图案例，如图二所示，这是一幅有向图，它的各个强连通分量在图中用灰色标记；我们的操作是将每个强连通分量看成一个顶点（比较大而已），那么会产生什么后果呢？我们的原始的有向图就会变成一个有向无环图！

ps:想一想为什么不能存在环呢？因为前提我们把所有的强连通分量看成了一个个顶点，如果顶点A和顶点B之间存在环，那A和B就会构成一个更大的强连通分量！它们本应属于一个顶点！

在得到一幅有向无环图（DAG）之后，事情没有那么复杂了。现在，我们再回想一下我们的目的————在图一中，我们希望区域二先进行dfs，也就是箭头指向的区域先进行dfs。在将一个个区域抽象成点后，问题归结于在一幅有向无环图中，我们要找到一种顺序，这种顺序的规则是箭头指向的顶点排在前！

到这儿，我们稍微好好想想，我们的任务就是找到一种进行dfs的顺序，这种顺序，是不是和我们在前面讲到的某种排序十分相似呢？我想你已经不难想到了，就是拓扑排序！但是和拓扑排序是完全相反的。

我们把箭头理解为优先级，对于顶点A指向顶点B，则A的优先级高于B。那么对于拓扑排序，优先级高者在前；对于我们的任务，优先级低者在前（我们想要的结果就是dfs不会从优先级低的地方跑到优先级高的地方）

对于图二：我们想要的结果如图三所示：

如果我们从顶点1开始进行dfs，依次向右，那么永远不会发生我们不希望的情况！因为箭头是单向的！

我想，到这儿，你应该差不多理解我的意思了。我们还有最后一个小问题————如何获取拓扑排序的反序？

其实解决方法很简单：对于一个有向图G,我们先取反（reverse方法），将图G的所有边的顺序颠倒，然后获取取反后的图的逆后序排序（我们不能称为拓扑排序，因为真实情况是有环的）；最后，我们利用刚才获得的顶点顺序对原图G进行dfs即可，这时它的原理与上一篇文章无向图的完全一致！

最后，总结一下Kosaraju算法的实现步骤：

• 1.在给定的一幅有向图 G 中，使用 DepthFirstOrder 来计算它的反向图 GR 的逆后序排列。
• 2.在 G 中进行标准的深度优先搜索，但是要按照刚才计算得到的顺序而非标准的顺序来访问
  所有未被标记的顶点。

具体的实现代码只在无向图的实现CC类中增加了两行代码（改变dfs的顺序）

package Graph.Digraph;

public class KosarajuSCC 
{ 
   private boolean[] marked;   // 已访问过的顶点 
   private int[] id;           // 强连通分量的标识符 
   private int count;          // 强连通分量的数量
   public KosarajuSCC(Digraph G) 
   { 
      marked = new boolean[G.V()]; 
      id = new int[G.V()]; 
      DepthFirstOrder order = new DepthFirstOrder(G.reverse()); //重点
      for (int s : order.reversePost()) //重点
         if (!marked[s]) 
         {  dfs(G, s); count++;  }
    }
   private void dfs(Digraph G, int v) 
   { 
      marked[v] = true; 
      id[v] = count; 
      for (int w : G.adj(v)) 
         if (!marked[w]) 
             dfs(G, w); 
   }
   public boolean stronglyConnected(int v, int w) 
   {  return id[v] == id[w];  }
   public int id(int v) 
   {  return id[v];  }
   public int count()
   { return count;}
}

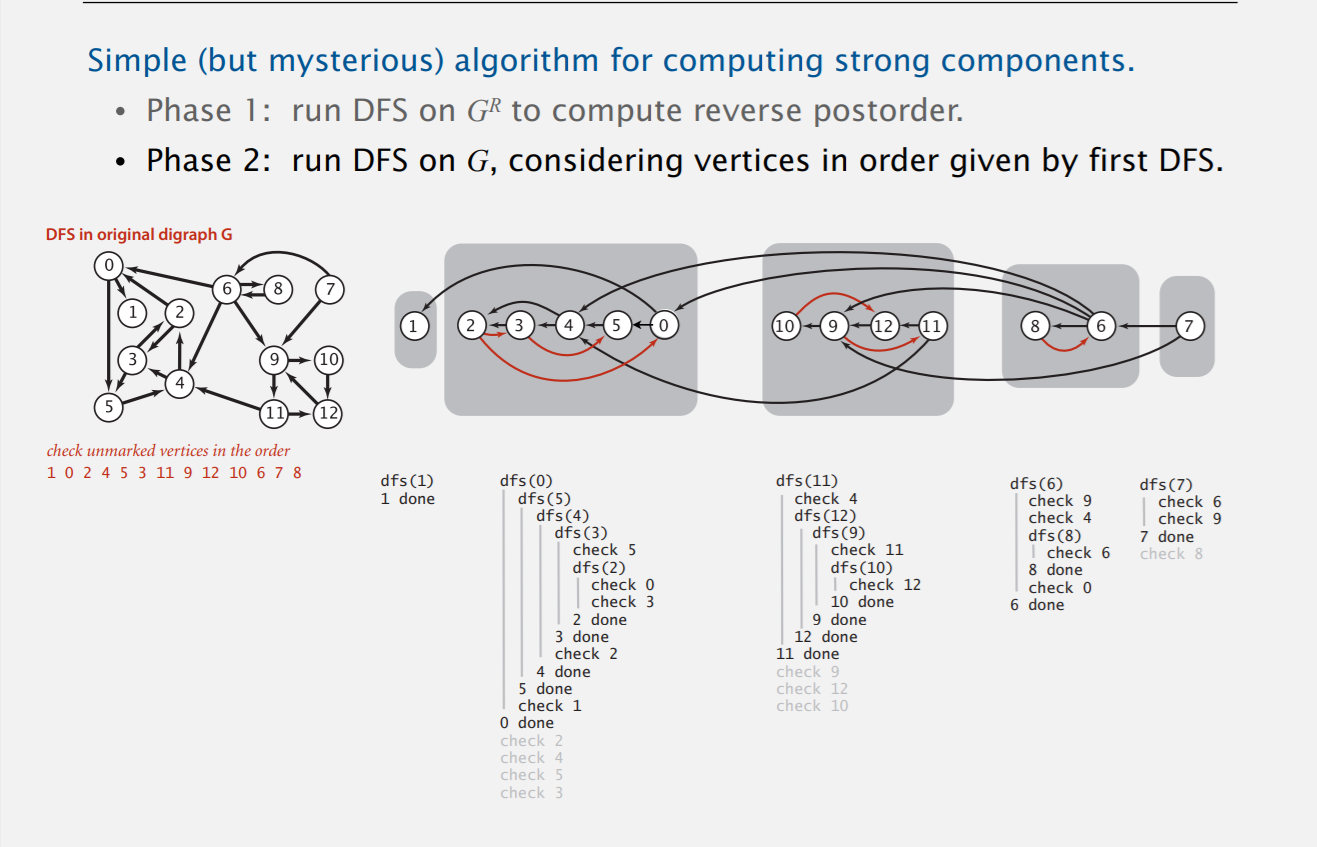
最后，附上一幅具体的操作过程：

有了Kosaraju算法，我们很容易能够判断

• 给定的两个顶点的连通性（上文代码stronglyConnected)
• 该图中有多少个强连通分量（上文代码count)

全文完