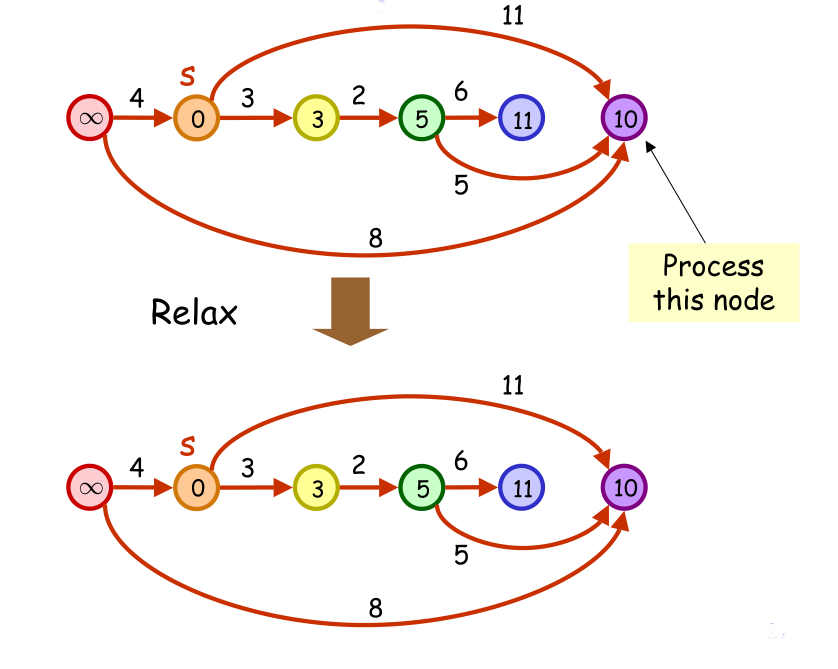
最短路径之如何理解“松弛”or“放松”?
地图软件是如何计算出最优出行路径的?一切要从relaxation:“松弛”or“放松”说起~
最短路径问题的目的是找到从一个顶点到达另一个顶点的成本最小的路径。最短路径算法被广泛地应用于解决各种复杂的问题,比如在地图中寻找两个地点之间的最短路径,如何在网络连接中为路由器寻找最短的传输路径等等。为了实现最短路径算法,人们发明了一系列的算法,比如:Dijkstra算法与Bellman-Ford算法。但是这些算法都基于一个被称为放松的基本操作
relaxtion,有些人称为松弛,我就直接简单翻译为放松了,别管怎么叫,理解就行
在这篇文章中,我会详细介绍放松操作,同时给出解决最短路径问题的基本(通用)思想。
这篇文章的大纲是:
- 1.什么是最短路径问题?
- 2.怎样理解边的放松?
- 3.边的放松顺序重要吗?
- 4.无环加权图的最短路径算法
1.什么是最短路径问题?
我们接下来要讨论的问题被称为单源最短路(Single-Source Shortest Path),通俗来讲,就是给定一幅加权图和一个特定的顶点s,称为源;我们的目标是对于图中任意一点v,计算从源s到达v的最短路径
G=(V,E)是一个加权图
- 图G中的边有权重
- 可以为有向或者无向
- 可以是连通的或者不连通的
- 取
s作为一个特殊的顶点——叫做源
目标:对于图中任意一点v,计算从源s到达v的最短路径
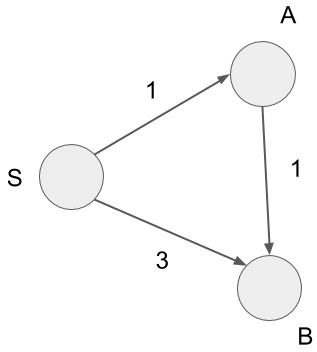
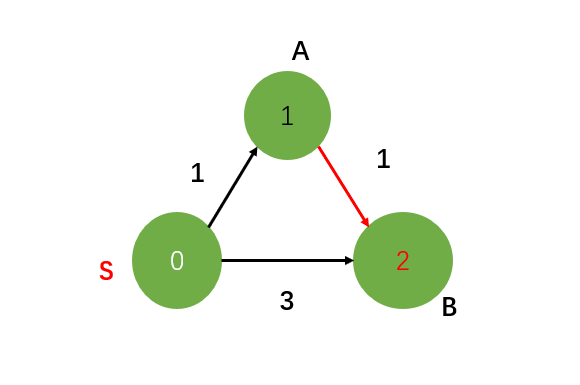
我们一起来看一个例子:
在这幅图中,我们取源s,对于顶点A,从s到达A的路径只有一条SA,所以最短路径就是SA,最小权重为1;对于顶点B,从s到达B的路径有两条:SB与SAB,显然最短路径是SAB,最小权重为1+1=2。
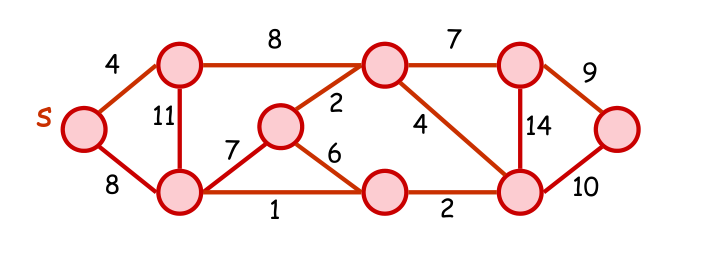
对于下面这幅图呢?
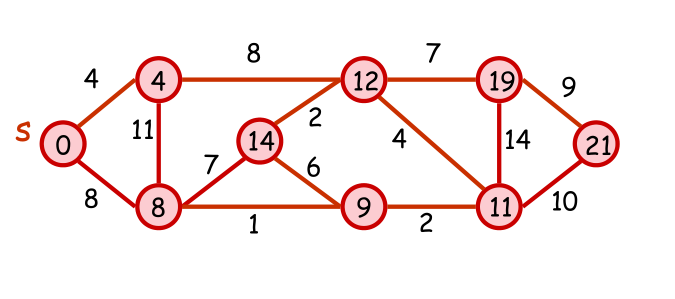
我们把最小权重写在每个顶点内部会得到图二,这就是我们的目标!
2.怎样理解边的放松?
现在,我们就来一起看一下放松这一个最基本最重要的操作吧!
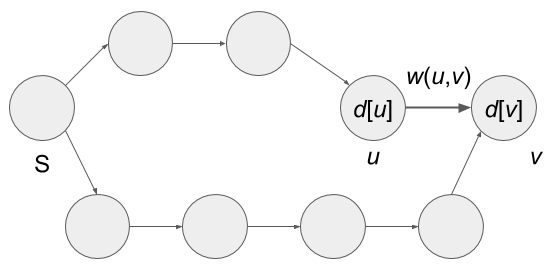
对于一条从
顶点u指向顶点v的边u-->v来说,如果满足 d[u]+w(u,v)<d[v],就更新d[v],使得d[v]=d[u]+w(u,v);这就是对边uv的一次放松操作;
其中,w(u,v)表示边的权重,d(u)表示顶点u到达源s的最短距离(目前已知)
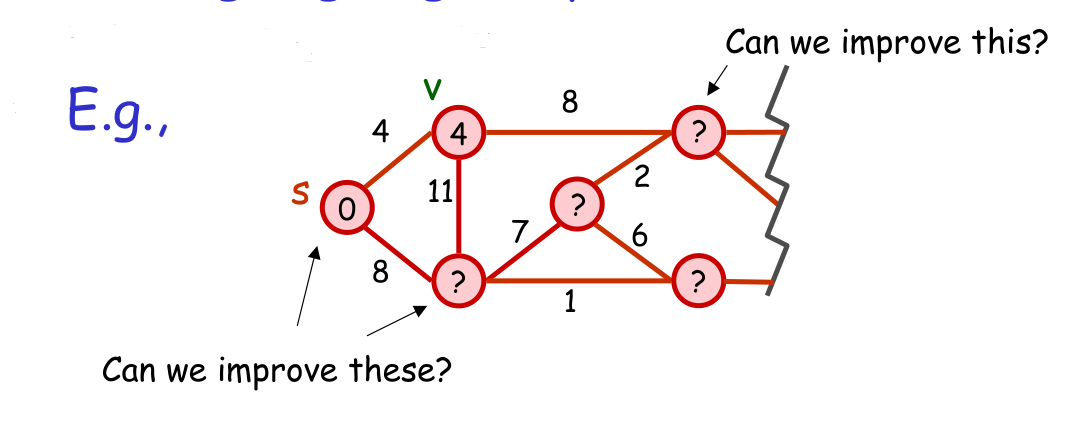
以下图为例,通过这次放松,我们有可能能够改进d[v]!顶点 v 原本有一个最短路径值d[v],它是在我们没有掌握足够多的信息的情况下做出的临时判断,d[v]可能真的是最终的答案也可能不是。我们就是通过对边uv进行放松操作来看一下能不能改进。如果d[u]+w(u,v)<d[v]成立,也就意味着我们找到了一条更近的路径到达顶点v,这条路径是通过顶点u的那条。所以,我们就更新顶点v储存的值d[v],同时还要更新路径信息,使得edgeTo[v]=u
上面就是放松的定义,它的实质就是判断一个顶点能不能有更好的选择,已知的最短路径能不能更短;如果满足那个不等式,就说明我们可以找到一条更好的路径,就更新它,改进它!
上面我们谈到的是对边的放松,但是在实际的代码实现中,我们的操作是对一个顶点进行放松。这儿理解起来很自然,对一个顶点进行放松就是对所有从该顶点发出的边进行放松的总和
在上图中,我们对顶点v操作中,对它相邻的三个边进行放松,其实质就是在问相应边对面的顶点————“你能够被改进(更短)吗?”
在了解了放松这个操作之后,我们就来看一下如何利用放松来求最短路径,下文以一个很简单的图来举例
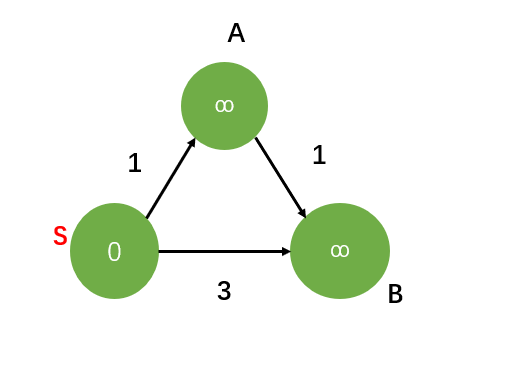
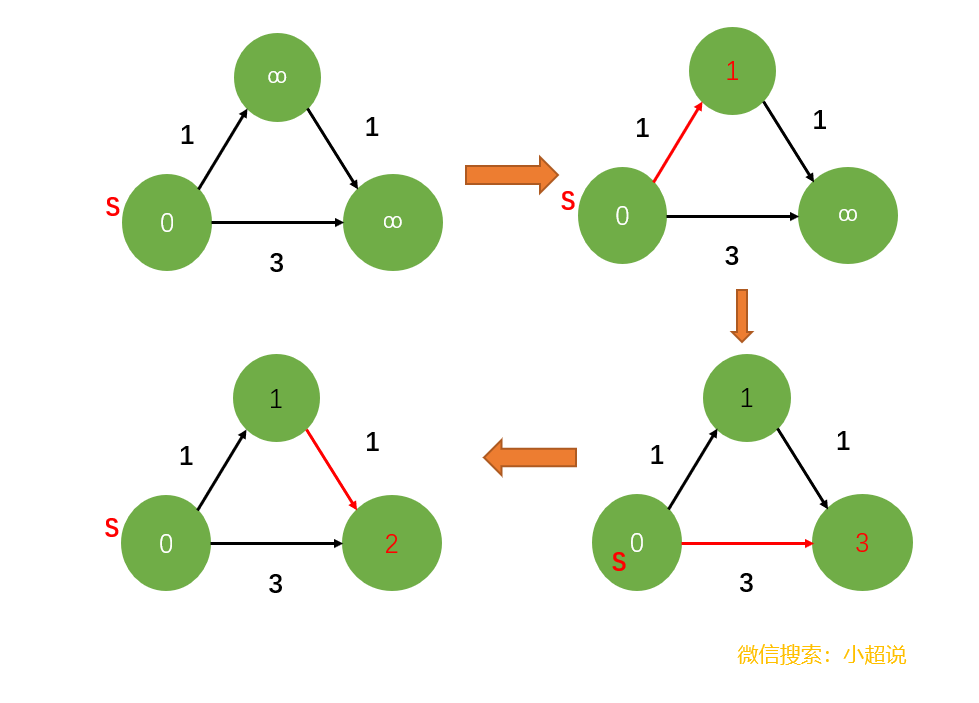
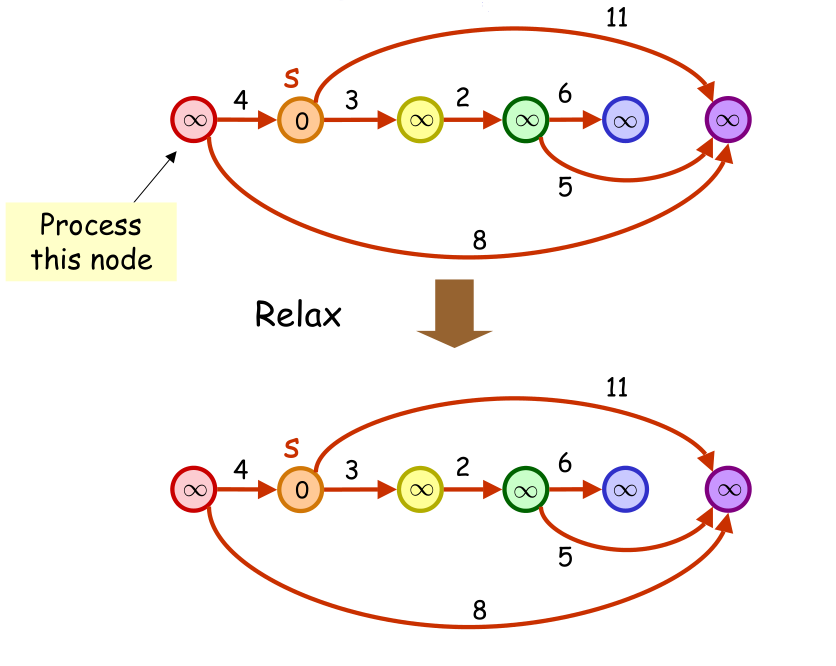
我们首先将所有的顶点的值d[v]标记为无穷大(因为我们还不能到达这些顶点),源s特殊处理标记为0,即d[s]=0,因为源s距离自身的距离显然为0
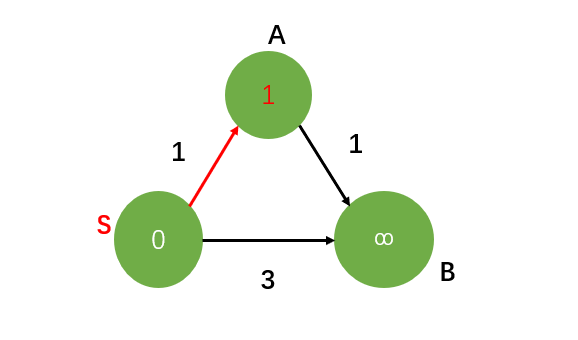
接下来,我们对顶点s进行放松。也就是对每一个从顶点s发出去的边进行放松,分别是SA与SB。先对SA放松,因为d[s]+1<∞,符合放松的条件,放松边SA同时使edgeTo[a]=s,得到图二
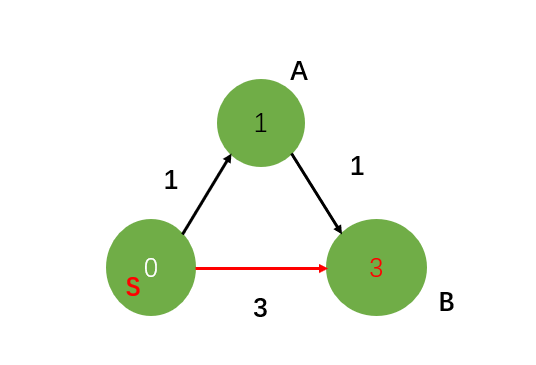
然后对边SB放松,同样因为d[s]+1<∞,符合放松的条件,放松边SB,同时使edgeTo[b]=s得到图三
很容易发现,图三并不是最终的答案:SAB边要比SB边短,然后,对顶点A进行相同的放松操作,得到图四即为最终的最短路径,同时改变edgeTo[b]=a。
图五就是操作的全部流程:
最后,我们可以通过edgeTo[]数组来得到所有的最短路径。比如根据edgeTo[b]=a得到顶点B是从顶点A过来的;而再根据edgeTo[a]=s得到顶点A是从顶点S处过来的,由此溯源了一条从S到达B的完整路径!
3.边的放松顺序重要吗?
在上面的篇幅我们讨论了使用放松操作获得最短路径的一个简单示例,我们从前往后依次对顶点S和A进行放松。但是由于我们的示例实在是太简单了,就没有重视放松的顺序!在这里,我想说的是,对于一个比较大的图(至少顶点不再是简简单单的三个),边的放松顺序重要吗?或者说不同的放松顺序能够达到相同的目的(求最短路径)吗?答案是否定的!
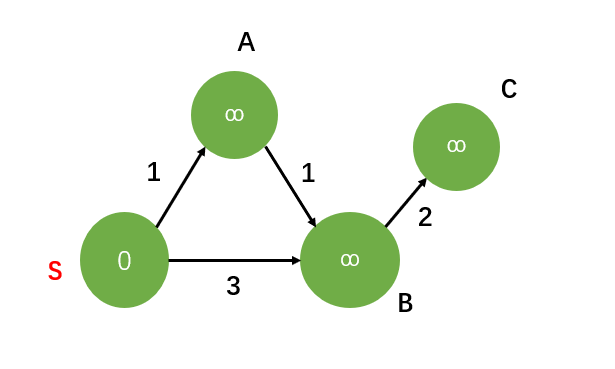
我们还是以一个例子说明这件事情:顺序很重要!
在图中,如果你先放松顶点S,再放松B,C最后放松顶点A就会出现问题!你会发现,当放松完顶点B后,d[c]=5,最后对A放松并不会影响d[c]=5的事实;所以,最后我们得到到达C的最短路径的值为5,然后实际上并不是这样,从图中不难看出,最小值是SABC,为4!
或许从听到我这个问题你就感觉到顺序是有要求的,现在更加证实了你的想法,记住:放松的顺序很重要!
我们随后要讨论的好几种最短路径算法,都是在研究放松的顺序!比如:
Dijkstra算法
如何决定边的放松顺序主要取决于图的性质【有环无环】【有无负权重边】
接下来我们就以无环加权图为例来看一下具体的实现过程。
4.无环加权图中的最短路径算法
算法:先对图进行拓扑排序,然后按照拓扑顺序放松顶点
我感觉伪代码更能体现思路,所以在下面给出了伪代码,具体的代码实现可以看一下算法4:
1 | DAG-Shortest-Path(G, s) |
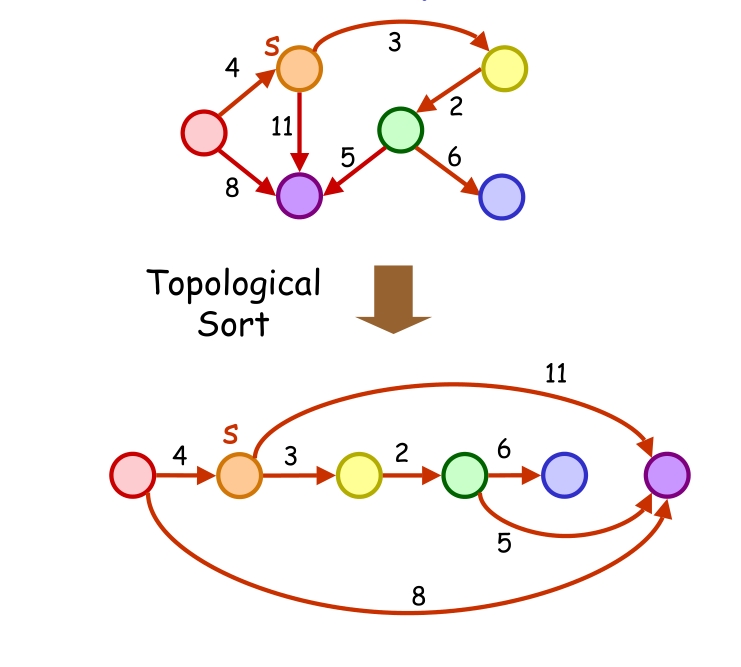
首先对原图进行拓扑排序,得到顶点的拓扑顺序,见【图一】
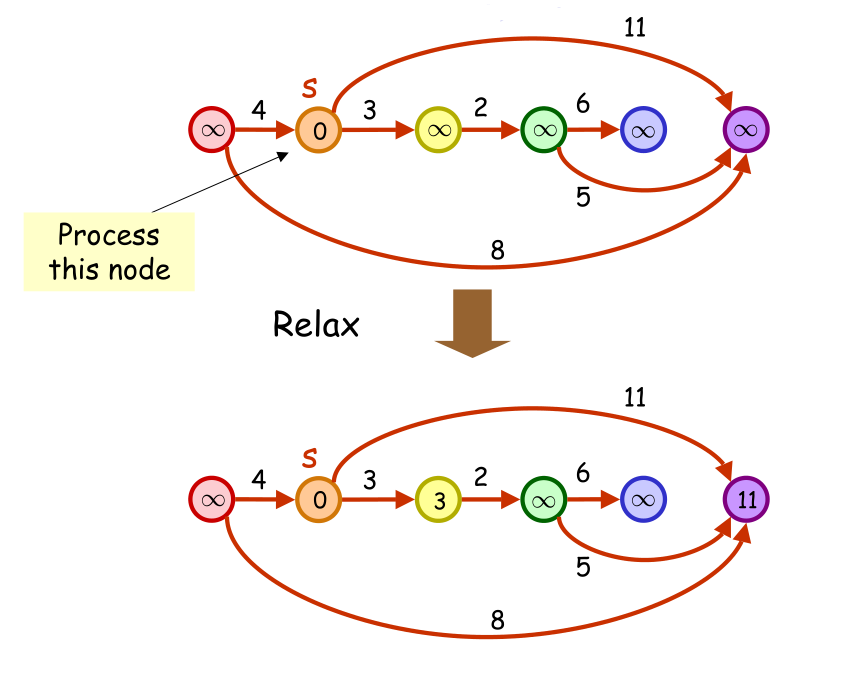
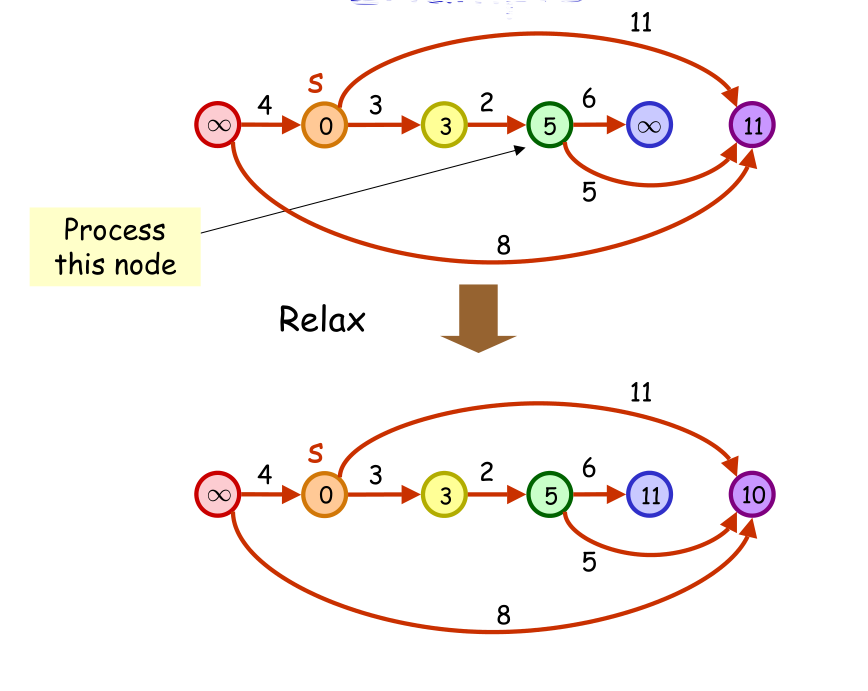
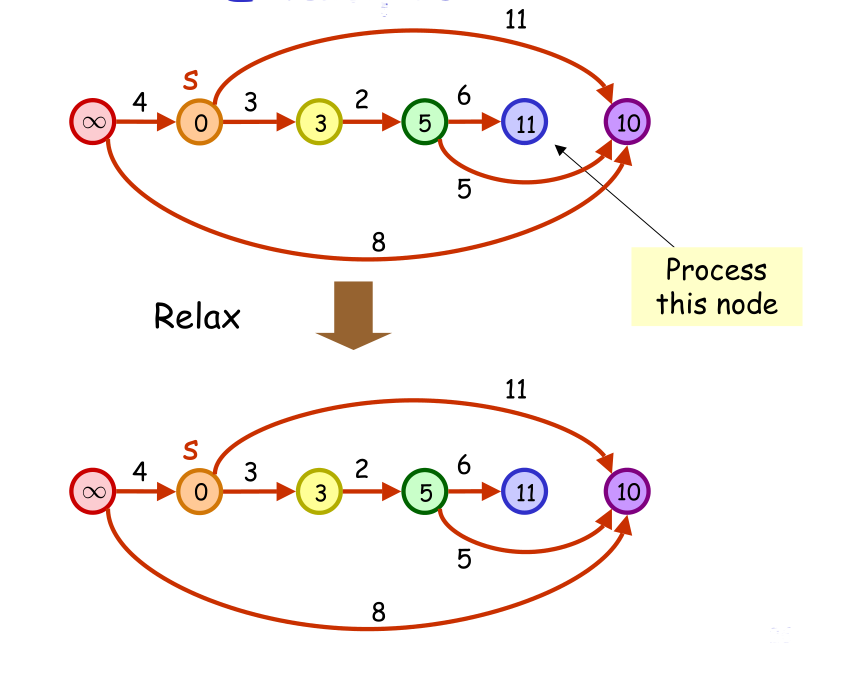
然后,将源顶点的距离初始化为0,其他顶点的距离值初始化为∞,从左向右依次对每个顶点放松
至此,按照拓扑顺序放松了所有顶点,最短路径也就求出来了。注意:该算法有两个比较重要的性质:
- 1.能够处理负权重的边
- 能够求出最长的路径(只需要将原图的所有权重取反即可)
参考:Understanding Edge Relaxation for Dijkstra’s Algorithm and Bellman-Ford Algorithm
全文完