什么是“图”？

我们从柯尼斯堡的七桥问题着手，开始介绍图算法的相关内容,这个问题是基于一个现实生活中的事例：河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？它被认为是图论的起源。

1、背景

Seven bridges of Königsberg

欧拉在1735年提出，并没有方法能圆满解决这个问题，他更在第二年发表在论文《柯尼斯堡的七桥》中，证明符合条件的走法并不存在

欧拉把实际的抽象问题简化为平面上的点与线组合，每一座桥视为一条线，桥所连接的地区视为点。这样若从某点出发后最后再回到这点，则这一点的线数必须是偶数，这样的点称为偶顶点。相对的，连有奇数条线的点称为奇顶点。由于柯尼斯堡七桥问题中存在4个奇顶点，它无法实现符合题意的遍历。

之后，不少数学家都尝试去解析这类事例。而这些解析，最后发展成为了数学中的图论233。

2、图的概念

图的定义：图是由一组顶点和一组能够将两个顶点相连的边组成的

图是一种非线性表数据结构，图中的元素我们叫做顶点，图中建立的连接关系我们叫做边。，图主要分为四种：无向图、有向图、加权图、加权有向图。

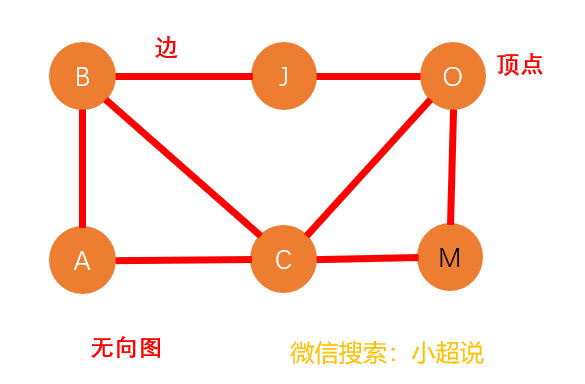
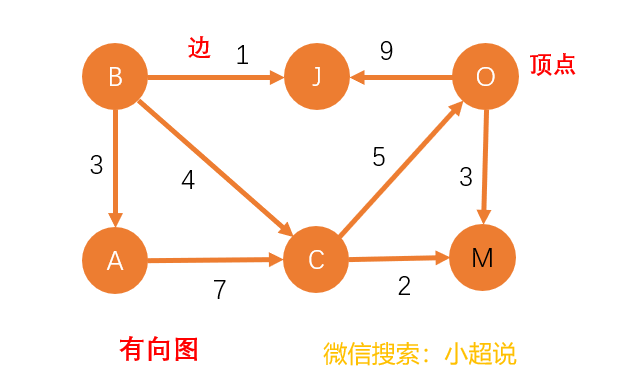
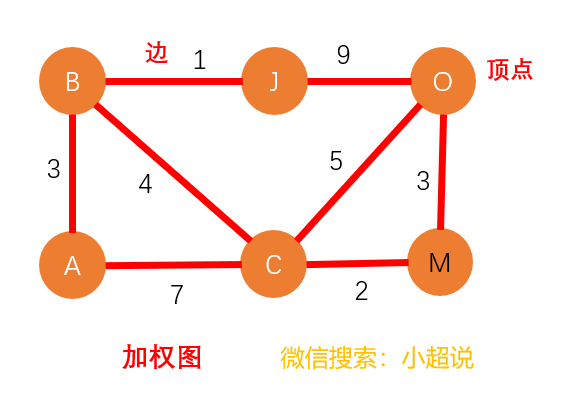
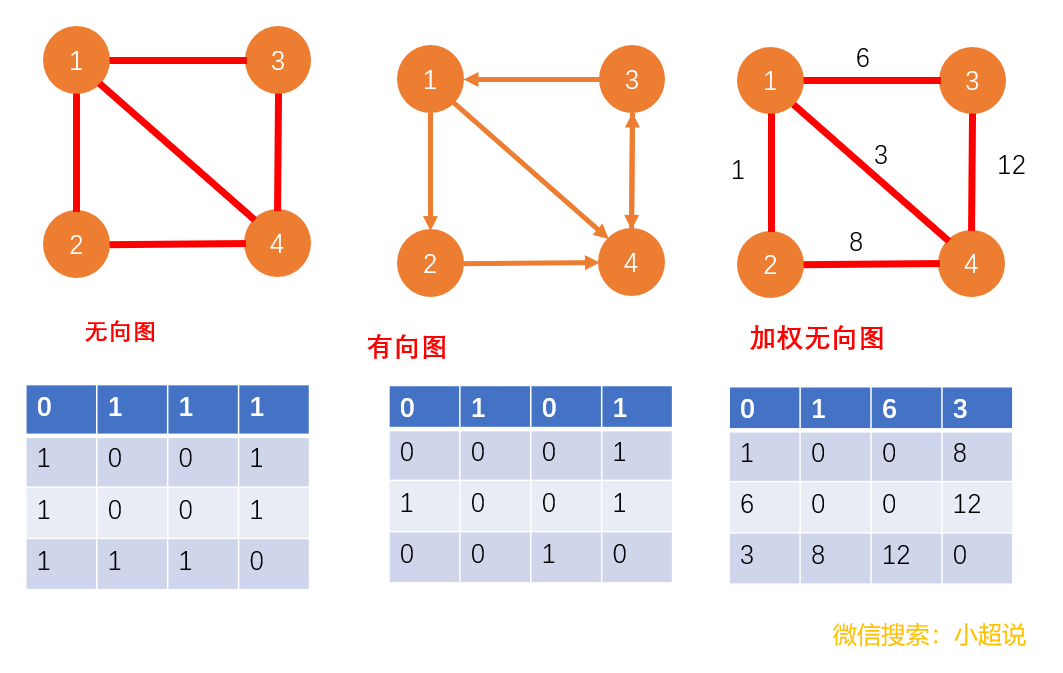
我们把有边有方向的图叫做“有向图”，把边没有方向的图叫做“无向图”，把边带有权重的图叫做“加权图”，这些概念其实都比较容易理解，你可以参考下面的几幅图对比一下。我们可以分别类比生活中的：知乎关注（有向）、微信交友（无向）和QQ好友亲密度（带权值）。

在图的表示中，我们定义度的概念。对于无向图而言，一个顶点的度是指跟该顶点相连接的边的条数；对于有向图而言，我们分别定义入度和出度，顶点的入度表示有多少条边指向这个节点，顶点的出度表示有多少条边以这个节点为起点指向其他节点。

3、图的存储方法

图的存储方法主要有两种：邻接表（Adjacency List）和邻接矩阵（Adjacency Matrix）。我们首先来介绍一下这两种存储方法。

1.邻接矩阵

邻接矩阵，顾名思义，就是利用矩阵去描述图，它的底层依赖于一个二维数组。对于无向图而言，如果顶点i与顶点j之间有边，那么我们就把A[i][j]和A[j][i]标记为1，它们之间没有边就标记为0；对于有向图而言，如果顶点 i 到顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，那我们就将 A[i][j]标记为 1。同理，如果有一条箭头从顶点j 指向顶点 i 的边，我们就将 A[j][i]标记为 1。对于带权图，数组中就存储相应的权重。

我们使用邻接矩阵来表示图，虽然的确很直观明了，但是却比较浪费空间。

其一，对于无向图来说，A[i][j]永远等于A[j][i]，我们只需要使用一半矩阵就可以成功地表示，那另一半空间就被浪费掉了；

其二、如果我们存储的是稀疏图，也就是顶点很多，但每个顶点的边并不很多，此时邻接矩阵的存储方法就更加浪费空间了。好比微信有好几亿的用户，对应到图上就是好几亿的顶点。但是每个用户的好友并不会很多，一般也就几百个而已。如果我们用邻接矩阵来存储，那绝大部分的存储空间都被浪费了。

总结一下，当图为稀疏图、顶点较多，即图结构比较大时，更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时，使用邻接矩阵作为存储结构较为合适。

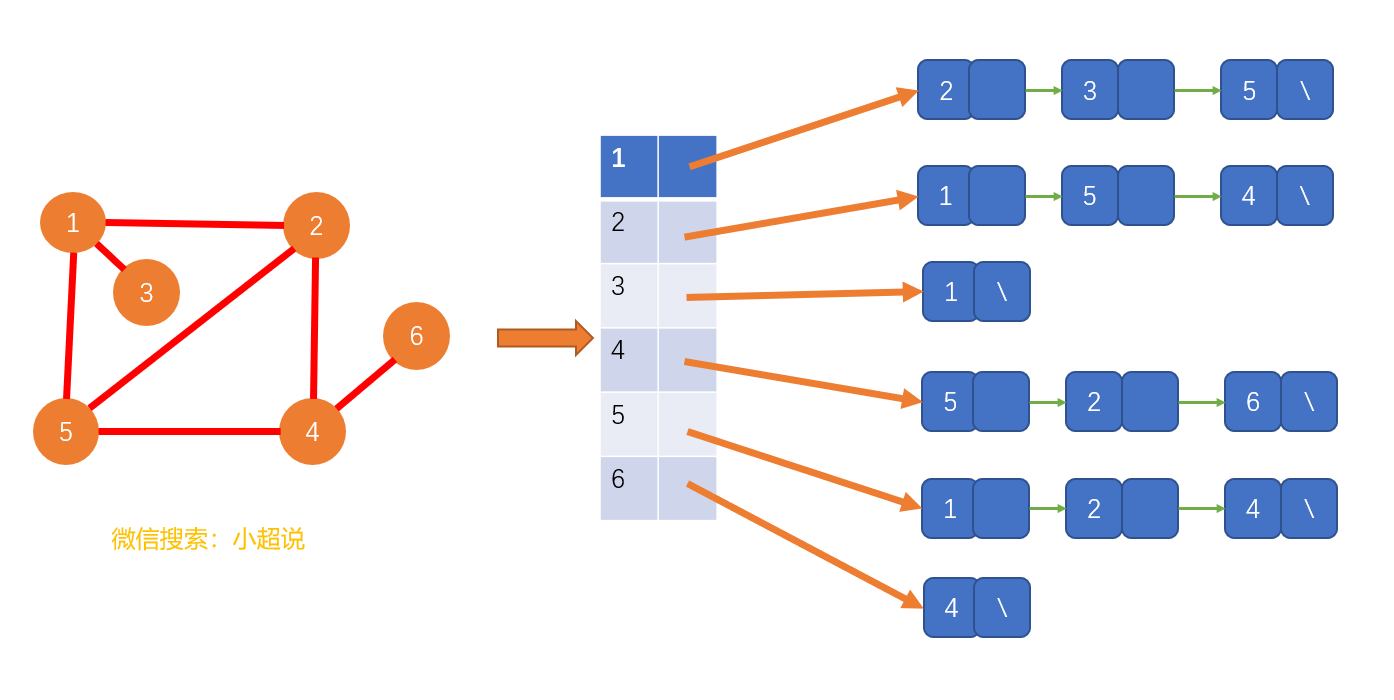
2.邻接表

我们使用一个以顶点为索引的列表数组，其中数组中的每个元素都指向一个单独的链表，该链表存储了与数组中顶点相邻的所有顶点。有点绕口，不过我为你准备了一张图，我相信结合图片你肯定可以更好地理解。

相比于邻接矩阵，邻接表比较节省存储空间，但是使用起来却比较耗费时间。不过，它的形式更为自由和灵活，比如，在链表过长的情况下，我们可以把链表用平衡二叉查找树（红黑树）替代，这样的话就比较高效了。

3.代码实现

public class Graph{
    //无向图
    private int v;//顶点的个数
    private LinkedList<Integer> adj[];//邻接表
    
    public Graph(int v){
        this.v=v;
        adj=new LinkedList[v];
        for(int i=0;i<v;++i){
            adj[i]=new LinkedList<>();
        }
    }
    
    public void addEdge(int s,int t){
        //无向图一条边存两次
        adj[s].add(t);
        adj[t].add(s);
    }
}